
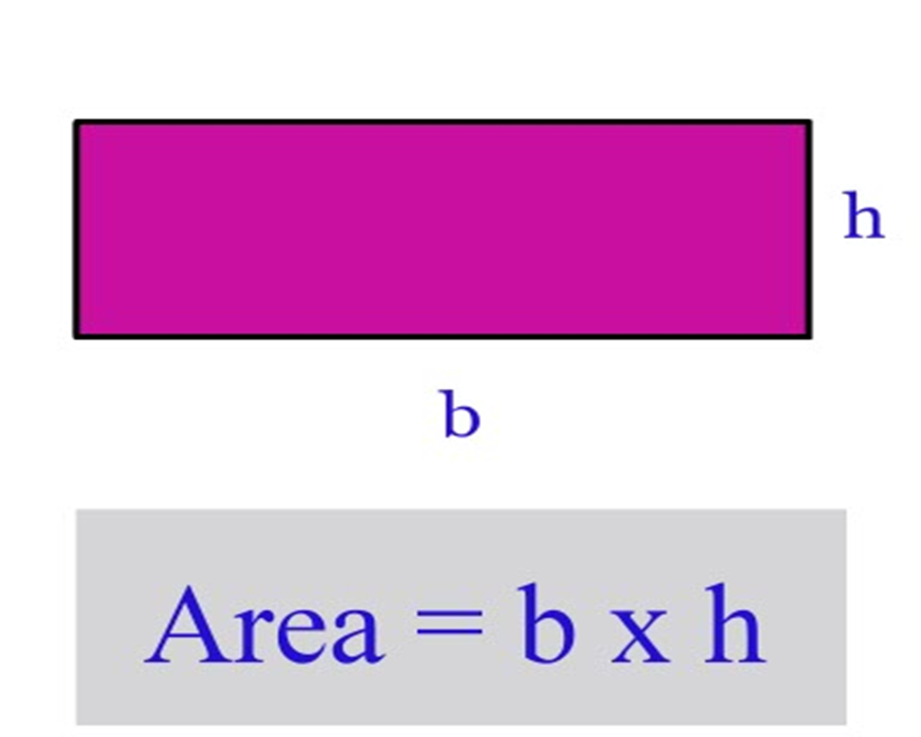

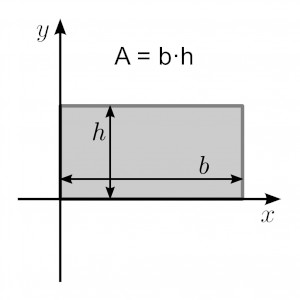
We can use the formula of the area of a rectangle to find the space occupied by these objects. Some examples of rectangular shapes are the flat surfaces of laptop monitors, blackboards, painting canvas, etc. In other words, the space occupied by a rectangle is the area of the rectangle. Taking too long to orchestrate the reasoning involved.The area of a rectangle is the number of unit squares that can fit into a rectangle.A correct way to say it would be, “The number of squares in one row is the same as the number of length units in the edge of the rectangle.” Maybe it sounds convoluted, but in mathematics, words mean things you have to combine the words into statements that are true, or at least not hostile to the distinction at hand. One book says, “The number of squares in one row is the same as the length in unit squares of the rectangle.” What is an object’s “length in unit squares”? Unit squares are area units, not length units. An example of this would be blurring the distinction between iterations of length units along the boundary and iterations of area units just inside the boundary. Being unclear about the difference between area and length.You can’t relate two ideas you don’t grasp individually. Then it isn’t clear what a length measurement means, or what an area measurement means. Doing a poor job with basic measurement concepts.Then the book has no chance of doing a proper job with area, or with anything else that relies on multiplication. Doing a poor job establishing what m × n means altogether.Some drawbacks I have seen in the way some math textbooks teach A = L × W: This is what is meant by “Area equals length times width.” The number of unit squares needed to tile a rectangle equals the number of length units that fit along one side multiplied by the number of length units that fit along an adjacent side. This argument is pretty obviously sound for any rectangle whatsoever with whole-number side lengths, so we can say that for any such rectangle: Remembering what × means, the total number of squares must then equal 7 × 5. For example, the 7 strips would turn into 7 groups of 5 squares each. If we draw both sets of lines, then each of the strips gets divided into squares (question: why perfect squares?). We might have done the same thing on either of the two adjacent sides, which would have resulted in the number of strips being 5. There are as many strips in the rectangle as there are length units in the side. If one side of the rectangle consists of 7 length units, then we can draw lines to divide the rectangle equally into 7 strips. In the context of a rectangle with, say, length 7 units and width 5 units, what are the groups, and what are the things? Today let’s confine our analysis of the formula to whole numbers, because I’m thinking about the formula today from the perspective of a young student who hasn’t yet absorbed fractional quantities or fraction operations. For whole numbers, the simple interpretation of m × n is that it stands for the number of things in m groups of n things each. The reason the formula works has to do with what the × symbol means. W is the number of length units when you measure an adjacent side of the rectangle.L is the number of length units when you measure one side of the rectangle.A is the number of unit squares needed to tile the rectangle.Has a student ever asked you why multiplying length by width gives the area of a rectangle? In this blog post, Standards co-author Jason Zimba describes the area formula on a conceptual level and highlights some weaknesses in the ways textbooks introduce the formula. Editor’s Note: This blog post originally appeared on Jason Zimba’s personal blog on August 10, 2016.


 0 kommentar(er)
0 kommentar(er)
